“最強の関数”ってナンだ!? 数式ごとに項を比較して強さを決める動画が登場。n次関数vs指数関数、指数関数vs階乗関数…バトルの結果に視聴者も謎の納得
今回紹介するのは、ア=ジさんが投稿した『【ゆっくり数学解説】100万ドルの難問へ P≠NP予想 番外編』という動画です。
投稿者メッセージ(動画説明文より)
21世紀最大の難問『P≠NP予想』について、ざっくりご紹介します。
数学ファンの方から数学にトラウマのある方まで楽しんでいただけます。
質問、リクエスト等ございましたら気軽にどうぞ。
今回はP≠NP予想とはあまり関係が無いです。ご了承ください。しかも内容薄い。
休憩の話題として、のんびり見ていただけると嬉しいです。


今回は関数の強さ比べの概念を様々な関数をとりあげて詳しく解説していきます。まず2つの関数の強さは、xを大きくしていき、もう大小が入れ替わらなくなったときの値の大きさを比べると比較できます。
そして強さの順は一次関数よりも二次関数、二次関数よりも三次関数の方が強く、n次関数よりもy=2^xやy=3^xといった指数関数、指数関数よりもy=x!といった階乗関数の方が強い。この強さ関係を、原則としてしっかり覚えておいてください。

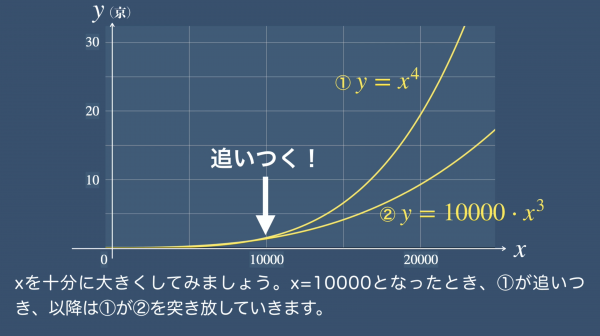
まずはy=x^4とy=10000x^3、どちらが強いでしょうか。グラフにしてみると②は10000倍しているだけあって、xが小さい時はとっても強そうなのですが、xを十分に大きくしていくとx=10000となったときに①が追いつき、以降は①が②を突き放していきます。
これは「強さ」の定義から①の方が強いとなります。

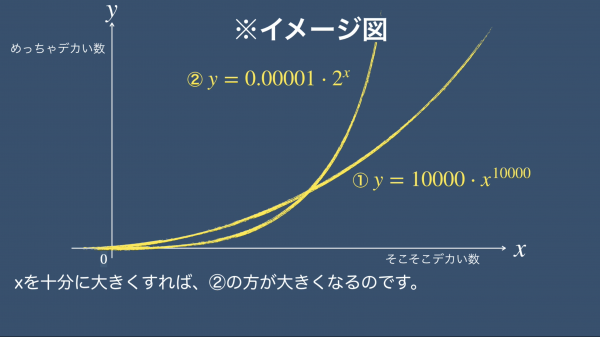
次は、y=10000x^10000とy=0.00001・2^xです。xを十分に大きくすれば、②の方が大きくなっていきます。

この例は少々極端ではありますが、こちらも「n次関数より指数関数の方が強い」という、原則通りです。いくら大きな数を掛けようが、関数自体の強さには敵いません。

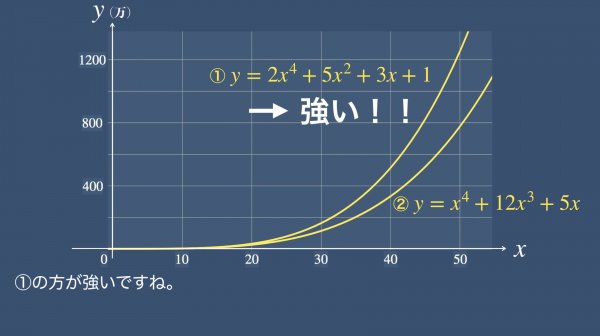
続いてこちら、y=2x^4+5x^2+3x +1とy=x^4+12x^3+5xではどうでしょう。グラフを見ると分かります。
①の方が強いですね。xが十分に大きいとき、x^3やx^2などの項はx^4に比べれば、誤差となっていきます。

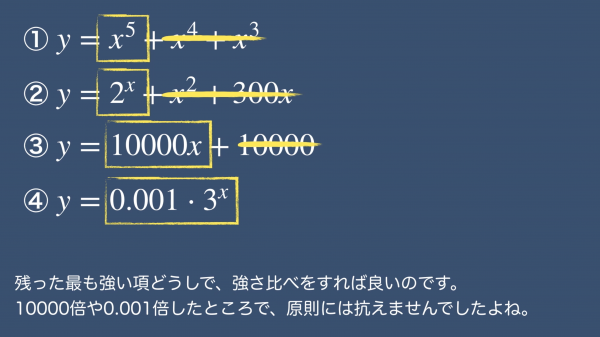
では確認テストです。これらの関数を強い順に並べてみてください。まずはそれぞれの関数ごとに最も強い項を見つけます。
xが大きくなれば、x以外の項は誤差となります。残った最も強い項同士で強さ比べをすれば良いのです。
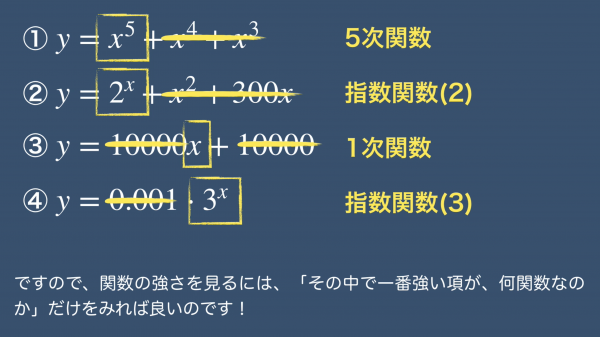
関数の強さを見るには「その中で1番強い項が、何関数なのか」だけを見れば良いのです。
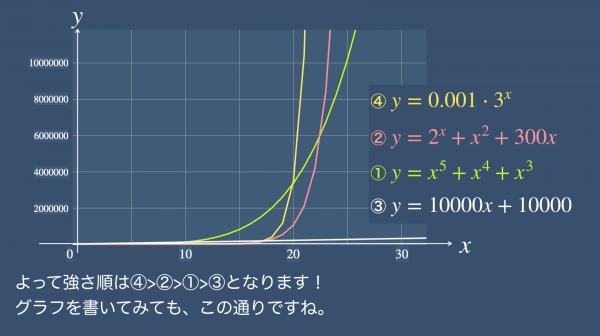
よって強さ順は④>②>①>③>となります。この関数の強さ順に「いくら修行しても素質ある奴には敵わないみたいな感じか」「頭良すぎて」「一度負けただけで永遠の敗者なのか」といった様々なコメントが寄せられました。
解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。
ーあわせて読みたいー
・スペースコロニーで野球ってできるの? 落下地点がずれてキャッチャーフライがホームランに!? ボールは壁面へ激突…物理の知識を総動員して計算してみた