35年間未解明だった「ABC予想」をやさしく解説してみた。証明されるメリットとは? 謎に満ちた数学の宇宙を覗いてみませんか
今回紹介するのは、えりまきおじさんさんが投稿した『【数学きりたん】きりたんと学ぶABC予想ってなんですか??』という動画です。
VOICEROIDの東北きりたんが、35年間未解明だった超難問「ABC予想」についての解説を行いました。
投稿者メッセージ(動画説明文より)
東北きりたんが数学の「未解決っぽい問題」であるABC予想について解説してくれます。
【追記】
ちゃんと 2^3 と書いてある、いいね?(種兄はケジメを受けた)
ちゃんと 281<rad(56*225*281) と書いてある、いいね?(種兄は朦朧とした)
正しくは「うちゅうさい」と読むそうです。そっかぁ…(種兄は塩を投げられた)
素因数分解をおさらい
「最も重要な未解決問題」と言われた超難問「ABC予想」が、2020年、ついに京都大数理解析研究所の望月新一教授により証明されました。投稿者のえりまきおじさんさんが、世界中の数学者を悩ませてきた「ABC予想」について、やさしく(?)解説していきます。

東北きりたん:
早速本題に入りましょう。みなさん「素因数分解」はご存知でしょうか。まずはそこからはじめたいと思います。次のふたつの数字を素因数分解してみましょう。

東北きりたん:
このように素数の積として分解することができました。

東北きりたん:
こうやって自然数を素数の積として分解することを「素因数分解」と言ったのでした。この時、このふたつのように、素因数の中に共通の素数がない場合、これらが「互いに素」というのでした。「互いに素」なもの、「互いに素でないもの」の例はこんな感じです。

東北きりたん:
「互いに素」という考えは日常生活でも必要になるとても大事なものなので、繰り返し眺めてしっかり感覚を掴んでくれると嬉しいです。
radの性質とABC予想の主張
東北きりたん:
さてここから「根基」-「radical」の話題に移っていきます。「radical」とは、各自然数に対して定まる、ある自然数です。厳密ではないのですが、黒板に実際の例を並べますので、そこでどういった数字のことなのかを掴んでいただけると幸いです。

東北きりたん:
元になる数字を7875だとすると、その根基であるrad(7875)は次のようになります。
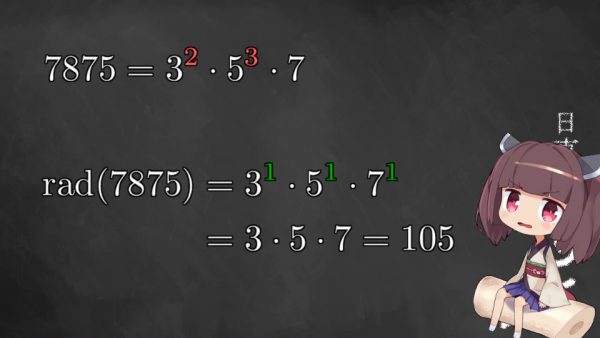
東北きりたん:
どのような操作をしたかおわかりになりますか。素因数分解したあと、累乗をすべて1乗に下げてしまったのです。他の例も見てみましょう。
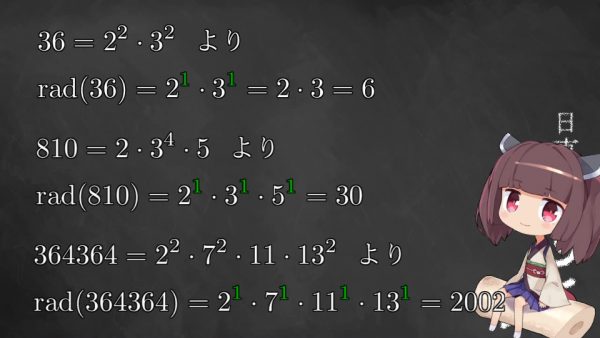
東北きりたん:
素因数分解をもとに、その要素をひとつずつ掛けた数字を作っているのがわかりますか。これがある自然数に対応するradの定義です。ABC予想とは、このradの性質についての問題なのです。その性質とは何か。では次の計算を見ていきましょう。ふたつの互いに素な自然数を用意して、その足し算と、3つの掛け算のradを計算します。


東北きりたん:
自然数ふたつの和と、それを含むに3つの積のradと大小を比較すると、radのほうが大きいですね。次の計算にいってみましょう。

東北きりたん:
今回もradのほうが大きいです。ではもうひとつ。

東北きりたん:
こちらもradのほうが大きいですね。実はこれが偶然じゃないというのが、ABC予想の主張なのです。まだほとんどの方が「どういうことだよ!」という感じだと思いますので、とりあえず私が思いついた、互いに素の数字の場合を並べて書いていきますね

東北きりたん:
もうこれ以上はいいでしょう。導かれる予想はこうです。

東北きりたん:
わかりますか? こうです!

東北きりたん:
AもBも自然数ですので、A+Bとしたとき、A×B×CのほうがCより大きいのが当たり前ですよね。ではこれをrad(abc)に置き換えても、同様に成り立つのではないか。これがABC予想の元々の部分です。
例外の存在
東北きりたん:
ではなぜ、黒板では「ほとんどの場合」と但し書きをしているのでしょうか。そうです、成り立たない例外があるのです。それらの例外を見ていきましょう。


東北きりたん:
このようにrad(abc)が綺麗に自然数の累乗になってしまう場合は、元のCよりrad(abc)のほうが小さくなることもあります。1はすべての自然数と互いに素であることには注意しましょう。実はこのような例外は、無限に存在することがわかっています。次の例を見てみましょう。

東北きりたん:
この通り、無限にある自然数から、同じ数だけ例外を作ることができます。実際にいくつか当てはめて計算してみましょう。

東北きりたん:
これを見ると、確かにCのほうがrad(abc)よりも大きいですね。Bが9の倍数になっていること。そしてCが綺麗に2の累乗になっていること。このふたつがきいて、rad(abc)がぐぐっと小さくなっているのがわかります。
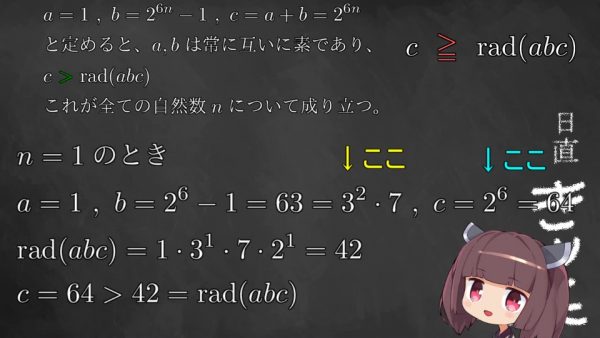
東北きりたん:
次も見てみましょう。Nが2の時も同じように、Bが9の倍数であること、Cが2の累乗であることがきいて、Cそのものより、rad(abc)のほうが小さくなっていることがわかります。
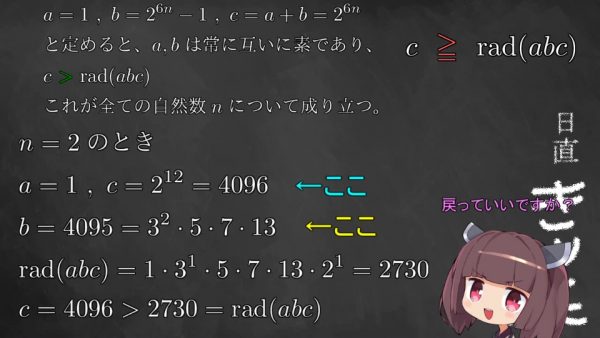
東北きりたん:
では本当にすべての自然数について、同じことが成り立つのか気になりますよね。本当はこの部分も詳しく解説したいのですが、もうだいぶ慣れてきているかと思いますので、概要だけ素早く黒板に載せますね。
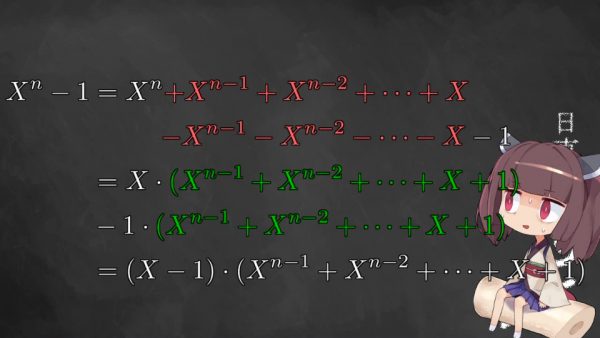
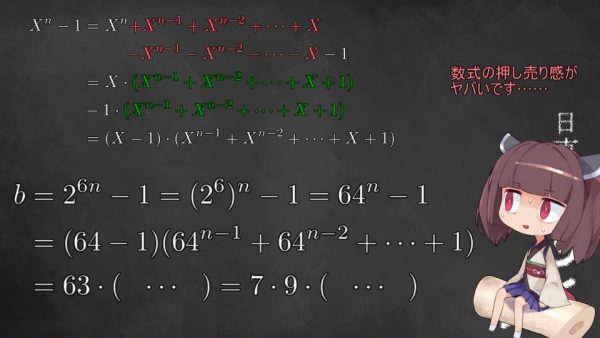
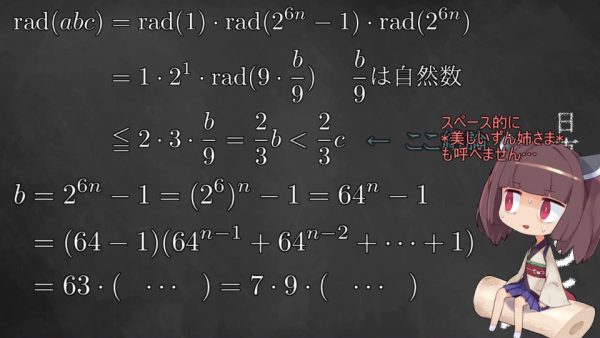
東北きりたん:
というわけで、みなさんご存知の通り、例外は無限に存在することが証明できるのでした。
ABC予想が正しいと何が嬉しいのか
東北きりたん:
前半はだいぶ数式マシマシでしたが、後半はお話が中心になります。ですので、ここからは肩の力を抜いて、コーヒーのお供に眺めるくらいに家で見てくだされば幸いです。まずはABC予想が成り立つ場合の応用についてです。ABC予想が正しいと仮定すると、様々な問題を簡単に証明できることがわかっています。いくつかの例をWikipediaのページから引っ張ってきました。

東北きりたん:
これらの例についても、軽く証明の概要などを付けたかったのですが、勉強不足で論文を読むのが辛いのと、動画に収めきれないという二重苦で、泣く泣く諦めました。興味を持たれた方がいましたら、是非Wikipedia日本語版の記事を見てほしいと思います。さて、例がすべて似たような形をしていることに気づきましたでしょうか。

東北きりたん:
だいたいこんな形の方程式に対する定理ばかりなのです。数学において、この形の方程式は非常によく現れ、総称して「楕円形(エリプティック)」などと呼ばれます。堆積学、代数学、幾何学と様々な場面に現れ、それらも問題の多くに応用できるということは、つまりABC予想そのものがエリプティックなものが持つ、本質的な性質なのではないか。

東北きりたん:
そんな類推ができるからこそ、ABC予想は単純に未解決問題のひとつというだけではなく、全世界が注目する重要な問題として、私たちの前に立ち続けているのです。
投稿日の2017年から3年の月日が経過し、2020年ついに日本の天才数学者・望月新一氏の歴史的快挙により証明された「ABC予想」。動画のコメント欄は「理論通りましたね おめでとう」「数学界の革命」「数学者って本当に凄いね」などと祝福と熱いコメントであふれかえっていました。
視聴者コメント
面白かった(理解できたとは言ってない)
日本語なのに理解が追い付かないぜ
数学は哲学とはよく言ったもんだ
なんで足し算と掛け算を比べる必要があるんですか(激怒)
役に立つか分からないけど好きだからやるんだよぉ!(数学専攻
わからんということがわかった、楽しかった
・“最強の関数”ってナンだ!? 数式ごとに項を比較して強さを決める動画が登場。n次関数vs指数関数、指数関数vs階乗関数…バトルの結果に視聴者も謎の納得