100円玉の周りに沿って別の100円玉を転がすと何回転する? なぜか回転数が増える仕組みをゆっくり解説
今回紹介する、グノもんさん投稿の『百円玉の周りにそって別の百円玉を転がすお話』という動画では、円周に沿って回転する円の回転数について解説を行っていきます。
円周は同じ長さなのになぜ回転数が増えるの?
図のように、100円玉の周りにそって、別の100円玉を滑らないように転がす。元の位置に戻るまでに何回転するでしょうか。一緒に解説を見ていきましょう。

ずんだもん:
まず紙を100円玉の周りに巻きつけて、一周したところで切る。この紙の端から100円玉を紙と滑らないように転がすと、一回転する。


次に100円玉をもう1枚用意して、この周りを滑らないように転がすと、途中で一回転して最終的に2回転する。紙の長さと100円玉の円周は同じ長さで、同じ長さに沿って移動したはずなのに、回る数が違う。不思議。
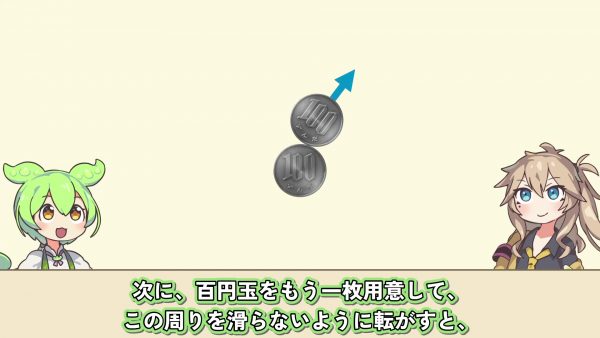
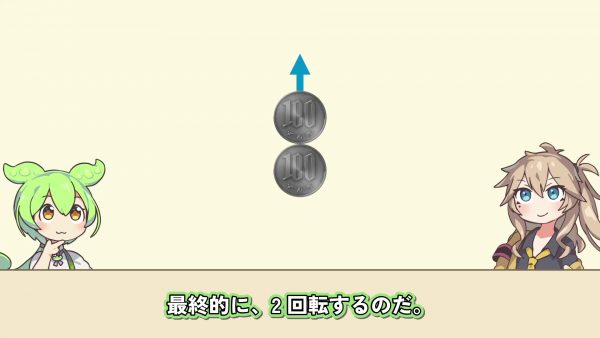
つむぎ:
確かに面白いね。だけど、どうしてこうなるのかわかったよ。実験してみよう。まず紙を少しだけ曲げて、その上を転がしてみる。するとまだ端に着く前に1回転して、端についた時には、さらに多く回った。

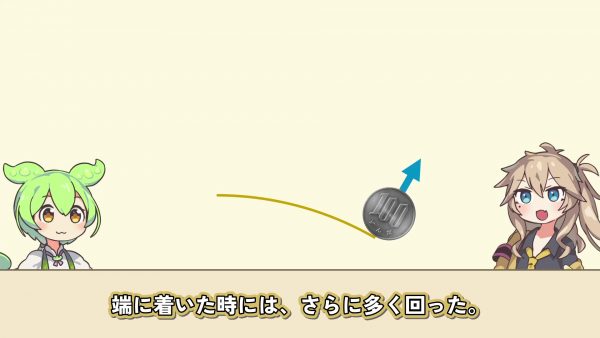
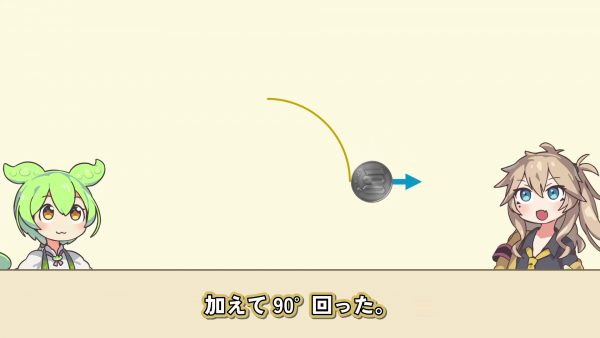
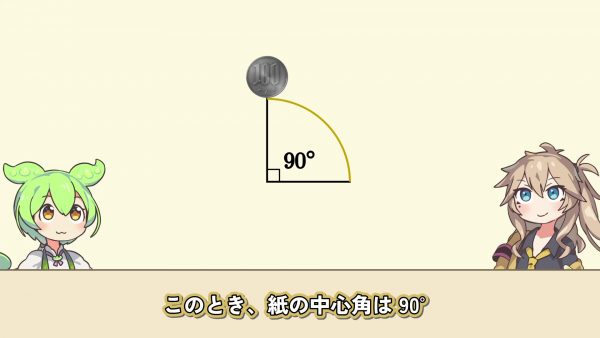
それならもっと大きく曲げてみよう。今度は100円玉の4倍の大きさの円に沿って紙を曲げる。この時、紙の中心角は90度。100円玉を転がすと、途中で360度回転し、加えて90度回った。
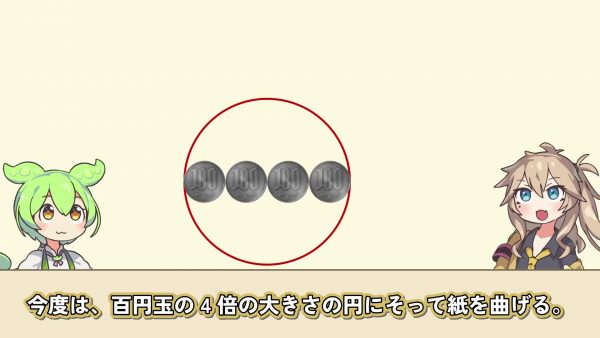
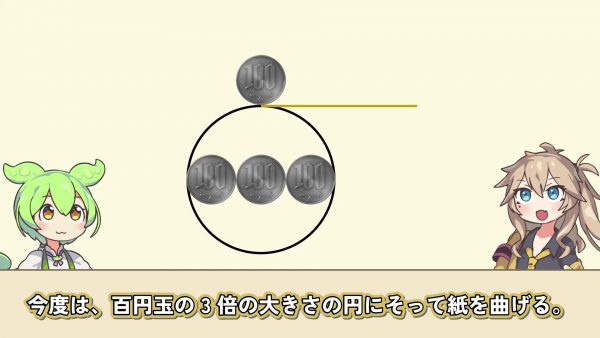
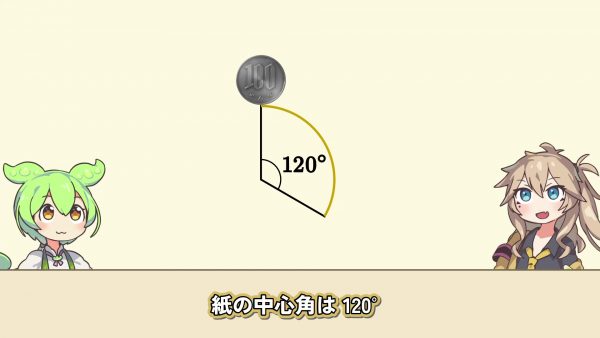
今度は100円玉の3倍の大きさの円に沿って紙を曲げる。紙の中心角は120度。100円玉を転がすと360度より120度多く回った。

ずんだもん:
中心角が大きくなるにつれて、100円玉の回る量が増えている。わかった、足し算だ。
つむぎ:
そういうこと。このように紙をもっと曲げて、100円玉と同じ大きさにすると、中心角は360度になる。100円玉を転がすと、360度に加えて、さらに360度、つまり2回転する。

ずんだもん:
2回転するのはわかったけど、動かしていない紙の形が影響するのは不思議だ。
つむぎ:
そうかな。相対的に考えてみたら? 例えば車が西から東へ走っているとき、車を中心に位置関係を考えると、車の外にあるもの全てが東から西へ動いているように見える。

今度は風車が時計回りに動いているとき、風車を中心に考えると周囲の者が反時計回りに動いて見える。回転方向が反対になることに注意してね。
今度は100円玉と同じ大きさの赤いコイン、青いコインと100円玉の円周と同じ長さの黄色い板を用意して、黄色い板の左端の上に赤いコインを、下に青いコインを置き、赤いコインを時計回り、青いコインを反時計回りに転がす。


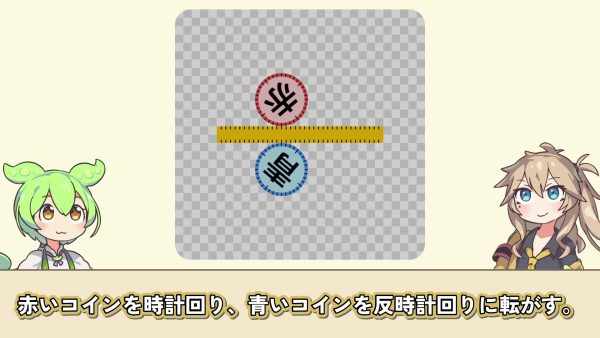
この状況を、青いコイン中心に考えると、青いコイン以外のものが時計回りに1回転して見える。
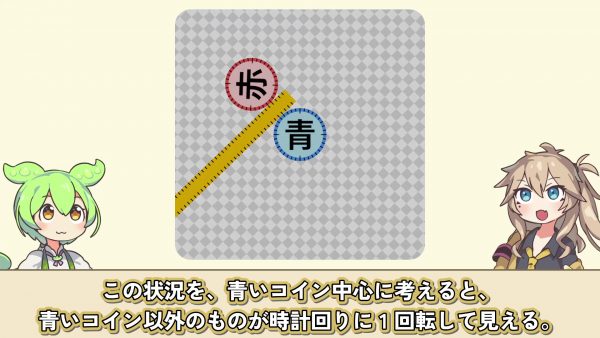
ずんだもん:
相対的だ。
つむぎ:
この黄色い板を細くしていくと、100円玉2枚の時と同じ状況になるよね。
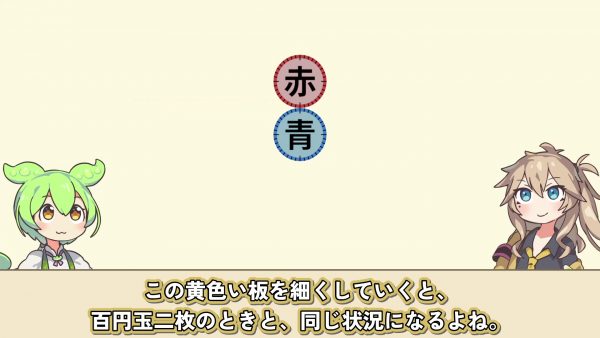
ずんだもん:
板の厚さは回転の数に影響しないの?
つむぎ:
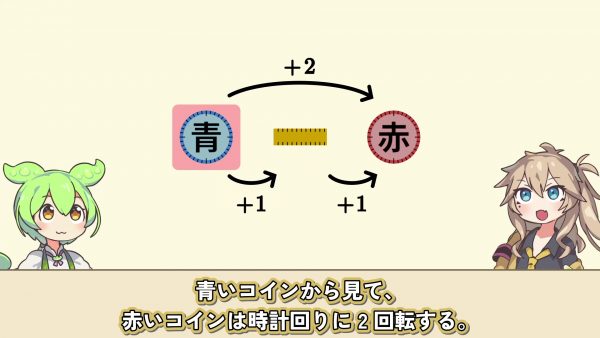
しないよ。実験してみてね。まとめると黄色い板から見て、赤いコインは時計回りに1回転、青いコインから相関的に見て、黄色い板は時計回りに1回転。青いコインから見て、赤いコインは計周りに2回転する。
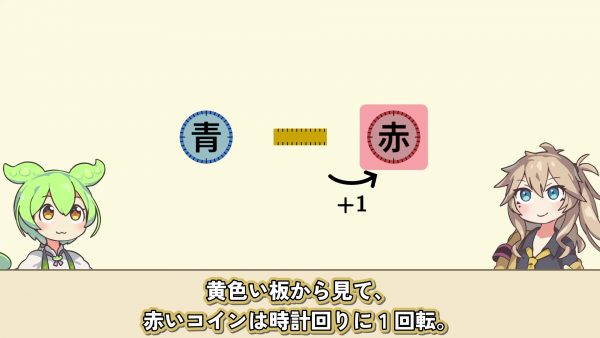
ずんだもん:
これって本当に足し算になるの?
つむぎ:
そうだよ。実生活ではなかなか経験できないかもしれないけれど、例えば遊園地のティーカップで土台の回転方向と同じ向きにカップを回すと、より勢いよく回るでしょう。
脳がバグを起こしそうな問題でしたが、相対的に考えると意外とすんなり納得できるのではないでしょうか。解説をノーカットでご覧になりたい方はぜひ動画をご視聴ください。
・「鉄1kgと綿1kgどちらが重い?」答えはもちろん…鉄に決まってるw←科学の知識を総動員した“屁理屈理論”に「これはすごい」の声
・“モンティ・ホール問題”を解き明かして数学的思考力を養ってみないか? 小学生でもわかるような丁寧な説明に「そうだったのか」と納得が止まらない