「多数決」って本当に公平なの? 全員が望まない結果を呼ぶかもしれない“投票のパラドックス”を解説してみた
今回紹介する、ワダイさんが投稿した『【ゆっくり解説】本当に納得ですか投票のパラドックス』では、音声読み上げソフトを使用して、一見正攻法に見える多数決が抱える「投票のパラドックス」について解説していきます。
勝ち抜き方式の多数決を使った裏ワザ
霊夢:
お昼ごはんを食べるなら何にしようか迷っていたのよ。やっぱり多数決で決めるのが一番かしら? それなら全員が納得したものを選べるもの。魔理沙:
霊夢、多数決は全員が納得したものになるとは限らない。全員が納得する方法に見えるが、多数決によって引き起こされる投票のパラドックスというものがあるんだ。霊夢:
投票のパラドックス?魔理沙:
今回は投票のパラドックスについて解説していく。わかりやすいように、実際に多数決をとってみよう。霊夢は何が食べたいんだ?霊夢:
そうね、カレーが食べたい気分だわ。魔理沙:
妖夢は何が食べたいんだ?妖夢:
わたしは蕎麦がいい。魔理沙:
そうか、私はラーメンが食べたいと思っている。

霊夢:
全員食べたいものが違ってしまったわね。魔理沙:
ではもう一度やり方を変えて多数決をとってみるぞ。カレーと蕎麦ならどちらが食べたいか選んでくれ。霊夢:
1対2でカレーが負けてしまったわ。

魔理沙:
では次に勝った蕎麦とラーメンならどうだ?

私が食べたかったラーメンに決まったな。カレーとラーメンならどっちが食べたいか選んでくれ。

霊夢:
やったわ。カレーが多数派ね。
魔理沙:
では勝ったカレーと蕎麦ならどっちを選ぶ?

霊夢:
今度は蕎麦を食べることに決まってしまったわね。どうしても私にカレーを食べさせたくないのかしら。魔理沙:
そういうことではない。2回連続で多数決したからそういうふうに感じるが、私がが違う結果になるように狙ってだしたからこうなったんだ。霊夢:
どうして1回目の時と結果が変わってしまったのかしら。魔理沙:
これが投票の順番によって起こるパラドックスのひとつだ。一見正しいように見える勝ち抜き方式の多数決に潜む罠なんだ。わかりやすいように食べたい順を図にするとこうなる。
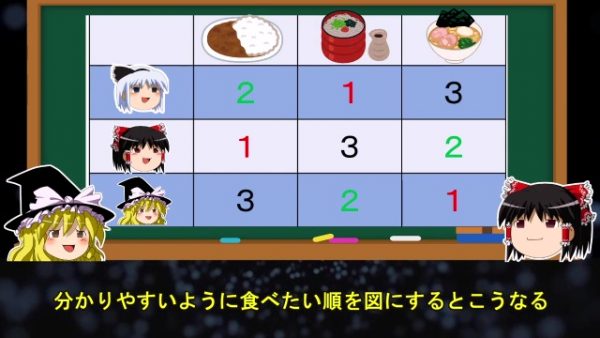
霊夢:
みんな食べたいものが見事にバラバラだったのね。魔理沙:
実はこのように順位にかぶりがない場合に、勝ち抜き方式の多数決を行うと、投票する順番によって結果が変わってしまうんだ。1回目に聞いたのはカレーと蕎麦だったが、この場合は1対2で蕎麦が多数派になる。次に残ったラーメンと蕎麦を多数決すると、最後に聞いたラーメンが多数派になるんだ。
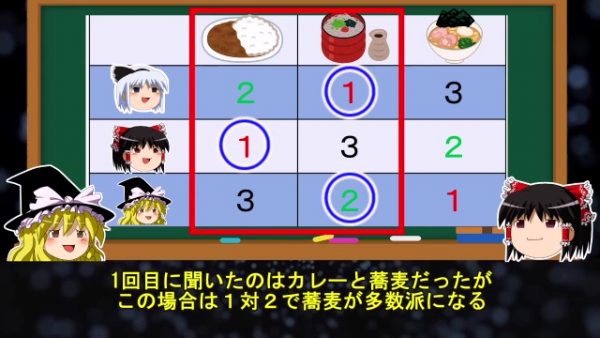
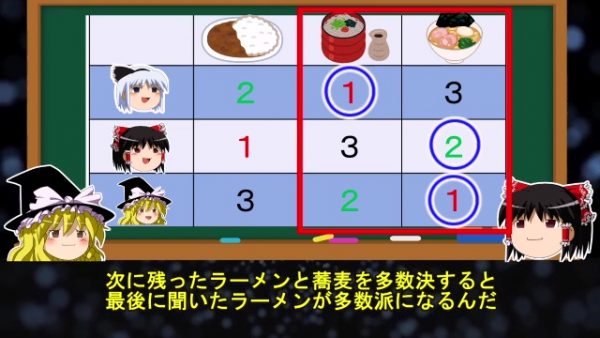
霊夢:
じゃ1回目に魔理沙が食べたかったラーメンに決まったのは……。魔理沙:
狙い通りだったってわけだ。霊夢:
じゃカレーが選ばれるようにするには、最初に蕎麦とラーメンから聞けばよかったということね。魔理沙:
そのとおりだ。霊夢:
天下一武道会のような勝ち抜け方式ではうまくいかないこともあるのね。
多数決が最悪の結果を生んでしまうケースも
魔理沙:
この他にも多数決で気を付けなければいけないことがある。今のは投票の順番によって順位が変わってしまうものだったが、他にも多数決で最もいい結果を選んだつもりなのに、最も悪い結果を選んでしまうことになることもあるんだ。 今度は人数を増やして7人で最も食べたいものをひとつ選んでみる。それでは全員の1位を見てみよう。
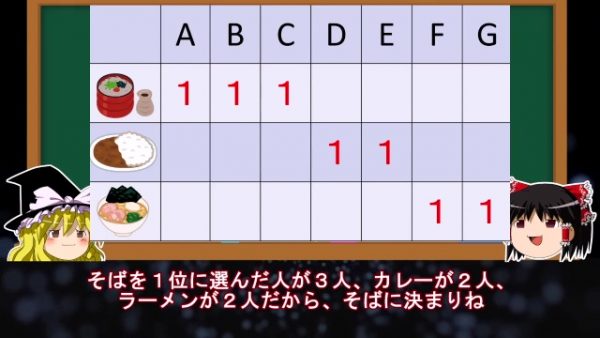
霊夢:
蕎麦を1位に選んだ人が3人、カレーがふたり、ラーメンがふたりだから、蕎麦に決まりね。自分が選んだものが食べられない4人は残念だけど、これのどこが最も悪い結果なのかしら。魔理沙:
では今度は全員の2位と3位も見てみよう。
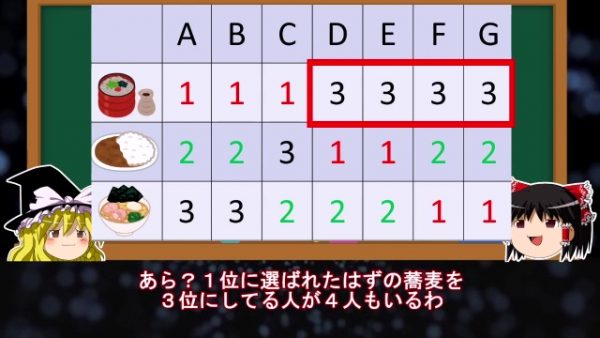
霊夢:
1位に選ばれたはずの蕎麦を3位にしている人が4人もいるわ。魔理沙:
質問は「最も食べたいものは?」だから、蕎麦が1位に選ばれた事実は間違いない。だが質問を「最も食べたくないものは?」と変えても蕎麦が1番に選ばれてしまう結果となっているんだ。集団で多数決をとって一番良いと思っていた結果が、実は一番悪い結果となっているとも見て取れるからな。霊夢:
みんなで選んで決めたのに、食べたくない人のほうが多かったなんて残酷ね。何か解決策はないのかしら。魔理沙:
解決策のひとつに総当り決選方式というものがある。この結果を元にして、二者択一で選ぶというものだ。わかりやすくいえば、最初にやった勝ち抜き方式のように2品ずつ競って確認をするんだ。まずは蕎麦とカレーの順位からは、このようにカレーが食べたい人が多いことがわかる。

次にカレーとラーメンではカレーのほうが多いということがわかる。

ラーメンと蕎麦ではラーメンが多いことがわかる。

こうやってすべての二者択一の組み合わせを試すことで、実は一番求められていたのがカレーだったということがわかった。あくまでこれは総当り決選方式を使って、捨て票の意思まで汲み取った結果だから、単記投票方式が間違っているということではないので、その点は注意してほしい。
勝ち抜け方式の多数決も単記投票方式にも便利な面もあるが、全員が望まない結果になったり、勝者が変わってしまう一面があることも覚えておかなければいけない。これが投票におけるパラドックス、投票の逆理と呼ばれる理由だ。
残念ながら結論を言ってしまうと、完全に欠点のない投票方式は存在しないと、アメリカの経済学者ケネス・アローによって数学的に証明されているんだ。
霊夢:
どのやり方にも何かしらの欠点は存在するということね。多数決や選挙で決まったものって一番正しいみたいに思っていたけど、結果だけでは汲み取れない部分や、やり方によって結果が変わってしまうこともあるのね。
民主主義的な手段としてよく使われる多数決ですが、場合によっては最悪の結果になるケースもあるなんて驚きです。より詳しい解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。
▼動画をノーカットで楽しみたい方は
こちらから視聴できます▼
―あわせて読みたい―
・有名な心理学実験「パブロフの犬」って結局なんだっけ? 「梅干しを見ると唾液」など“刺激と反応の条件づけ”のメカニズムをやさしく解説してみた