50年以上未解決だった数学の難問が解決されたかも? 狭い通路をギリギリ通せる最大の面積を求める「ソファ問題」を解説
今回紹介するのは、ニコニコ動画に投稿された『【VOICEROID解説】あの未解決問題がついに証明されたらしい【数学】』という、ゆーらしのさんの動画です。
投稿者メッセージ(動画説明文より)
Twitter(X)で話題になっていたので!
質問や指摘はいつでもお待ちしています。
数学の世界には、まだ結論が出ていない「未解決問題」がいくつもあります。
今回の動画で解説しているのは「ソファ問題」と呼ばれる未解決問題です。
ソファ問題とは、L字に曲がった通路を通り抜けられる図形の中で面積が最大のものは何か、という1966年に提起された数学の問題です。

幅を1とするL字に曲がった廊下があるとします。
この通路を通り抜けられる図形を考えていきます。
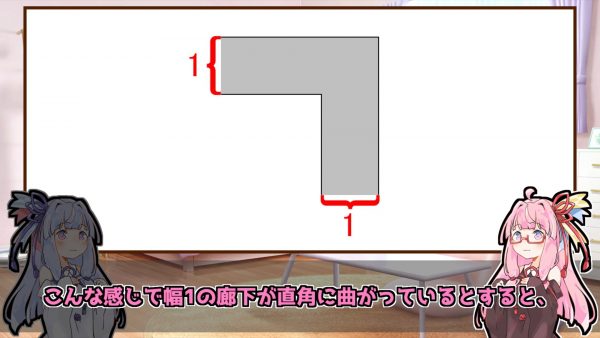
例えば縦横の辺の長さが1の正方形なら、通路を端まで進んで横にスライドさせれば通り抜けられます。



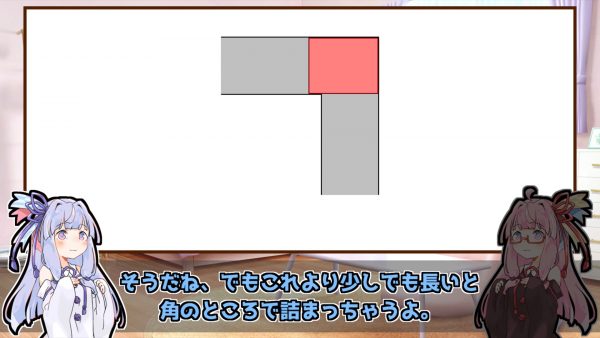
では、もっと面積を大きくしようとして横に伸ばすとどうでしょうか。
スライドして通り抜けようとしても、曲がり角で引っ掛かってしまいます。この形では通り抜けられません。
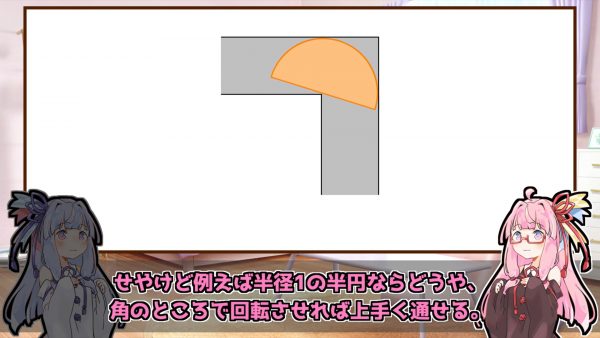
では、スライドではなく回転させて曲がり角を通ればどうでしょうか。
半径1の半円なら角を中心にぐるっと回して通り抜けられます。
面積は正方形が1×1=1、半円が1×1×π/2=π/2となり半円の方が大きくなっています。

では、どんな図形が最大の面積になるのか、という結論については今のところ分かっていません。
ソファ問題が提起されてから2年後の1968年に提案されたのが、こちらの受話器型の図形です。
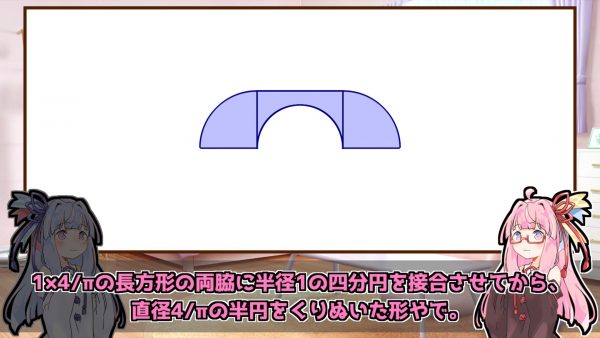
円を組み合わせた複雑な形ですが、L字の通路をするりと通り抜けられます。

ここからさらに24年後の1992年に提案された、より面積が大きい図形がこちら。

一見すると同じく受話器型ですが、18個の曲線が接続された複雑な図形となっています。
では、この図形が最大なのか? というと、それはまだ分からないままです。
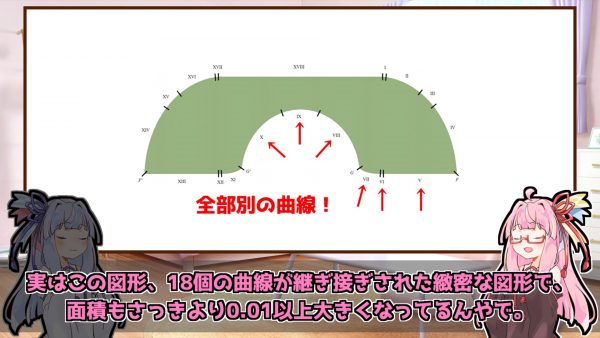
そして30年以上の月日が流れ、この受話器型ソファが、通路を通り抜けられる最大の面積を持つ図形であると証明する論文のプレプリント(正式な査読を受ける前の段階の学術論文)が、2024年12月2日に公開されました。
現段階ではまだ査読前ということで、証明に誤りが見つかるかもしれませんが正しいと確認されれば1966年から58年間未解決だった問題がついに解決することになります。
ソファがするりと通路を通り抜けられるアニメーションは分かりやすさと気持ちよさがありますので、ぜひ下記のリンクから動画でもお楽しみください。
▼動画はこちらから視聴できます▼
『【VOICEROID解説】あの未解決問題がついに証明されたらしい【数学】』
https://www.nicovideo.jp/watch/sm44393955
―あわせて読みたい―
・「マイナスを引くとプラスになる」を子供に説明できますか? 数学が苦手でも直感的に分かる解説に「なるほど、わかりやすい」
・450本の数式で吉田夜世『オーバーライド』のMVを再現してみた! 絵はグラフ描画ソフトで、音は波形を関数にして作った渾身の力作